Basic Drawing: FLine reference

`line += CFrame(...)`

Transforms this line by the coordinate system transform CFrame.

This page has more information on coordinate system transforms. You can also += a line with a Vector3 or a Vector2 as a shorthand for translation.

`.append(line, deep=0)`

Appends a line to this line.

You can optionally set the parameter deep=1 to completely dissociate the copied nodes from the original (otherwise the copies update with the originals).

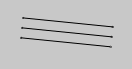
one = FLine().moveTo(10,10).lineTo(100,10)
two = FLine().moveTo(10,20).lineTo(100,20)
three = FLine().moveTo(10,30).lineTo(100,30)
all = FLine().append(one).append(two).append(three)
all += Vector2(200,1000)
all += CFrame(r=0.1)
_self.lines.add(all)

`.appendShape(shape)`

Appends a java2d Shape object to this line.

Java2D Shape objects are commonly found in other java drawing APIs (for example NodeBox2, Batik) and also built into Java.

Example

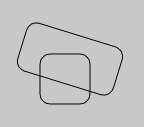
from java.awt.geom.RoundRectangle2D import Double

myRoundRect = Double(50,50,100,50,20,20)
line = FLine().appendShape(myRoundRect)
line += CFrame(r=0.3, center=Vector2(100,75))

myRoundRect2 = Double(70,70,50,50,20,20)
line.appendShape(myRoundRect2)

_self.lines.add(line)

`.appendVectorText2(text, x, y, font#"Gill Sans", attributes0, size=20)`

Appends (vector) text to this FLine with the specified font, attributes and size.

You can set attributes to be 1 for bold, 2 for italics and 3 for bold-italics.

Example

f = FLine().appendVectorText2("fuzzy", 0, 0, size=100)
f = f.newLineByResampling(100)
f = f.newLineByFilteringPositions2(lambda x,y : Vector2(x,y).noise(1+x*0.1))
f.filled=1
f.color=Vector4(0,0,0,0.3)
f.derived=1
_self.lines.add(f)

`.bounds2(fast=1)`

Returns the 2d bounding box of this line.

Set 'fast=0' to use a slower, exact algorithm. Otherwise, the bounding box is approximate. Returns a Rect instance.

Example

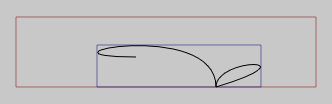
line = FLine().moveTo(20,20).cubicTo(-100,20,100,-20,100,50)
line.cubicTo(200,20,100,20,100,50)

bounds = line.bounds2()
boundingLine = FLine().rect(bounds.x, bounds.y, bounds.w, bounds.h)
boundingLine(color=Color4(0.5, 0, 0, 0.5))
_self.lines.add(boundingLine)

bounds = line.bounds2(fast=0)
boundingLine = FLine().rect(bounds.x, bounds.y, bounds.w, bounds.h)
boundingLine(color=Color4(0.0, 0, 0.5, 0.5))
_self.lines.add(boundingLine)

_self.lines.add(line)

`.bounds()`

3d version of bounds2

Returns (Vector3, Vector3) representing the (min, max) range of the positions and control nodes of this line.

Example

line = FLine().moveTo(20,20).cubicTo(-100,20,100,-20,100,50).cubicTo(200,20,100,20,100,50)

min, max = line.bounds()
approxCenter = (min+max)*0.5

`.circle(radius, x, y)`

Appends a circle to this line.

Example

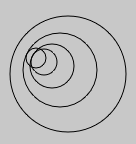
_self.lines.clear()

circles = FLine()
for n in range(0, 5):
    circles.circle( n*n*3+10, 8*n, n*4)

_self.lines.add(circles)

`.copy(deep=0)`

Makes a copy of this line

Copies have their own attributes and nodes positions.

Example

_self.lines.clear()
line1 = FLine().moveTo(10,10).cubicTo(50,-40,40,50,30,40)
_self.lines.add(line1)
line2 = line1
for n in range(0, 10):
    line2 = line2.copy()
    line2 += Vector2(20,0)
    line2 += CFrame(r=0.1)
    _self.lines.add(line2)

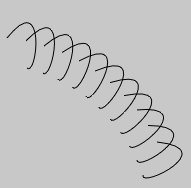
`.cubicTo(c1x, c1y, c2x, c2y, x, y)`

Draw cubic spline segment from current drawing position to x,y.

If you pass in 9 arguments rather than 6 you get a 3d cubic spline segment.

Example

line = FLine().moveTo(10,10).cubicTo(100,-20,10,50,100,100)
_self.lines.add(line)

c1 = FLine().moveTo(*line.nodes[0].position()).lineTo(*line.nodes[1].control1())
_self.lines.add(c1(pointed=1, pointSize=10, color=Color4(0.5, 0, 0, 0.5)))

c2 = FLine().moveTo(*line.nodes[1].position()).lineTo(*line.nodes[1].control2())
_self.lines.add(c2(pointed=1, pointSize=10, color=Color4(0.5, 0, 0, 0.5)))

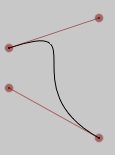
`.cursor(at=0)`

Returns a cursor for this line

The Cursor object can be used to interrogate the line at various positions. See here for more details.

Example

_self.lines.clear()

line1 = FLine().moveTo(10,10).cubicTo(100,-20,10,50,100,100)
line1.cubicTo(20,30,120,-10,20,-60)
_self.lines.add(line1)

cursor = line1.cursor()
while(cursor.currentD()<cursor.length()):
    _self.lines.add( FLine().moveTo(*cursor.position())(pointed=1))
    cursor.forwardD(10)

cursor = line1.cursor()
while(cursor.currentD()<cursor.length()):
    if (cursor.tangentForward()):
        t = cursor.tangentForward().rotateBy(Math.PI/2)
        mark = FLine().moveTo(*cursor.position())
        mark.relLineTo(*t)
        _self.lines.add(mark)
    cursor.forwardD(10)

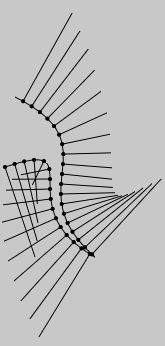
`.cursorAtPosition(*pos)`

Returns a cursor for this line that's at the position closest to pos

The Cursor object can be used to interrogate the line at various positions. See here for more details.

Example

_self.lines.clear()

line1 = FLine().moveTo(10,10).cubicTo(100,-20,10,50,100,100)
line1.cubicTo(20,30,120,-10,20,-60)
_self.lines.add(line1)

for n in range(0, 100):
    randomPosition = Vector2().noise(1)*140.0+(50,20)
    cursor = line1.cursorAtPosition(randomPosition)
    tri = FLine().moveTo(*cursor.position())
    tri.lineTo(*randomPosition)
    tri.relLineTo(*cursor.tangentForward()*0.1)
    tri.lineTo(*cursor.position())

    tri(filled=1, color=Color4(0,0,0,0.2))

    _self.lines.add(tri)

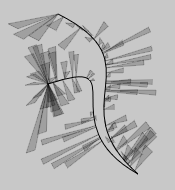
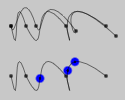
`.doIntersections2(otherLine)`

Intersects two lines and returns cursors at the intersection points

Example

_self.lines.clear()

line1 = FLine().moveTo(0,0)
for n in range(0, 3):
    line1.cubicTo(10+n*30, 50, n*15, -50, 15+n*40, 0)

line1(pointed=1, color=Color4(0,0,0,0.5))
_self.lines.add(line1)


line2 = FLine().moveTo(0,0)
for n in range(0, 3):
    line2.cubicTo(4+n*30, 20, 10+n*15, -50, 25+n*40, n*5)

line2(pointed=1, color=Color4(0,0,0,0.5))
_self.lines.add(line2)

line1_copy = line1.copy()
line2_copy = line2.copy()

line1_copy+=Vector2(0,50)
line2_copy+=Vector2(0,50)

intersections=line1_copy.doIntersection2(line2_copy)

_self.lines.add(line1_copy)

for n in intersections:
    dot = FLine().moveTo(*n[0].position())
    dot(pointed=1, color=Color4(0,0,1,1))
    dot(pointSize=10)
    _self.lines.add(dot)

`.ellipse(rx, ry, x, y)`

Appends an ellipse to this line

Example

_self.lines.clear()

el = FLine()
for n in floatRange(0, 8,100):
    el.ellipse( 5,n*n*3+10, 40+8*n+Math.random()*5, n*4)
    el += CFrame(r=Math.random()*0.07, center=Vector2(100,0))

el(color=Color4(0,0,0,0.3))
_self.lines.add(el)

`.newLineByFilteringPositions2(lamdba x,y : ...)`

`.newLineByFilteringPositions(lamdba x,y,z : ...)`

Returns a new line by applying a function the positions of this line

The function passed in should return a (x,y) pair (or Vector2) or a (x,y,z) tuple (or Vector3) in the 3d case. All positions and control points are filtered through the provided function.

Example

_self.lines.clear()

line = FLine().moveTo(20,20).cubicTo(-100,20,100,-20,100,50).cubicTo(200,20,100,20,100,50)

_self.lines.add(line)

for n in range(0, 20):
    noisedLine = line.newLineByFilteringPositions2(lambda x,y : Vector2(x,y).noise(n))
    noisedLine+=Vector2(0,50)
    noisedLine(color=Color4(0,0,0,0.3))
    _self.lines.add(noisedLine)

`.newLineByFilteringNodes2(func)`

`.newLineByFilteringNodes(func)`

Returns a new line by applying a function to the nodes of this line

This function is passed in sever arguments that describe each node of the line. There are several kinds of nodes that can be on a line — depending on whether it's at the start, end or between two cubic segments, or two line segments. The signature for this function should be:

def func(before, here, after, beforeIsCurve, afterIsCurve):
   ...

before and after are the incoming and outgoing control vertices. They might be None if these vertices don't exist (for example there is no incoming control vertex to a node that's a .moveTo and there's no outgoing control vertex to a node that's at the end of a line). In the case where the node is between straight lines, these "control vertices" don't really exist — we pick a point that divides the incoming and outgoing straight lines. You can detect this by looking at beforeIsCurve and afterIsCurve.

To filter the line, mutate in place before, here and/or after. In the 2d case they will be Vector2 and in the 3d case, Vector3.

_self.lines.clear()
from functools import partial

line = FLine().moveTo(20,20).cubicTo(100,-100,100,-20,100,50)
line.cubicTo(200,20,100,20,200,50)

_self.lines.add(line)

def nodeFilter(sm, before, here, after, beforeIsCurve, afterIsCurve):
    if (before and after):
        smooth = (after-before)*sm
        before[:] = here-smooth
        after[:] = here+smooth

    here.noise(10)

for alpha in floatRange(-0.5, 1.5, 20):
    newLine = line.newLineByFilteringNodes2(partial(nodeFilter, alpha))
    newLine += Vector2(0,100)

    newLine(color=Color4(0,0,0,0.4))

    _self.lines.add(newLine)

`.filterNodes2(func)`

`.filterNodes(func)`

`.filterPositions2(func)`

`.filterPositions(func)`

In place versions of the methods above

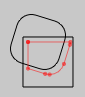
`line & otherLine`

Computes the intersection between two lines

Example

c1 = CachedLine().roundRect(30,300,50,50, 30)
c2 = CachedLine().rect(40,320,50,50)

c1 += CFrame(r=0.3, center=Vector3(55,325,0))

c3 = c1 & c2

c3(color=Vector4(1,0,0,0.5), pointed=1)

c3 += Vector2(4,4)
_self.lines.add(c1)
_self.lines.add(c2)
_self.lines.add(c3)

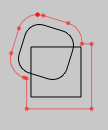
`line | otherLine`

Computes the union between two lines

Example

c1 = CachedLine().roundRect(30,300,50,50, 30)
c2 = CachedLine().rect(40,320,50,50)

c1 += CFrame(r=0.3, center=Vector3(55,325,0))

c3 = c1 | c2

c3(color=Vector4(1,0,0,0.5), pointed=1)

c3 *= Vector2(1.3, 1.3)
_self.lines.add(c1)
_self.lines.add(c2)
_self.lines.add(c3)

`line - otherLine`

Subtracts one line from another

Example

c1 = CachedLine().roundRect(30,300,50,50, 30)
c2 = CachedLine().rect(40,320,50,50)
c1 += CFrame(r=0.3, center=Vector3(55,325,0))

c3 = c1 - c2

c3(color=Vector4(1,0,0,0.5), filled=1)
_self.lines.add(c1)
_self.lines.add(c2)
_self.lines.add(c3)

`.lineTo(x,y [,z])`

Draws a line from the current position to (x,y)

You can optionally pass in a 'z' coordinate to draw in 3d.

Example

line = FLine().moveTo(10,10).cubicTo(100,-20,10,50,100,100)
_self.lines.add(line)

c1 = FLine().moveTo(*line.nodes[0].position()).lineTo(*line.nodes[1].control1())
_self.lines.add(c1(pointed=1, pointSize=10, color=Color4(0.5, 0, 0, 0.5)))

c2 = FLine().moveTo(*line.nodes[1].position()).lineTo(*line.nodes[1].control2())
_self.lines.add(c2(pointed=1, pointSize=10, color=Color4(0.5, 0, 0, 0.5)))

`.moveTo(x,y, [,z])`

Moves the cursor (without drawing) to the position (x,y)

You can optionally pass in a 'z' coordinate to draw in 3d.

While this doesn't draw any line (unlike, lineTo or cubicTo) it does draw points if the line is marked as .pointed=1 (see DrawingFLinesProperties).

Example

dots = FLine()
dots.pointed=1
dots.pointSize=10
for n in range(0, 100):
    dots.moveTo(Math.random()*100-50, Math.random()*100-50)
    dots.moveTo(*Vector2().noise(100))

_self.lines.add(dots)

`.newLineByResampling(numSamples)`

Roughly resamples this line to have 'numSamples' nodes. .

These new nodes are approximately spaced equally apart. For finer control and accuracy use a Cursor object — this will let you move forward and back along a line by a specified distance.

Example

f = FLine().appendVectorText2("r", 0, 0, size=500)
f2 = f.copy()
f2+=Vector2(200,0)
f = f.newLineByFilteringPositions2(lambda x,y : Vector2(x,y).noise(20))

f2 = f2.newLineByResampling(100)
f2 = f2.newLineByFilteringPositions2(lambda x,y : Vector2(x,y).noise(20))

_self.lines.add(f)
_self.lines.add(f2)

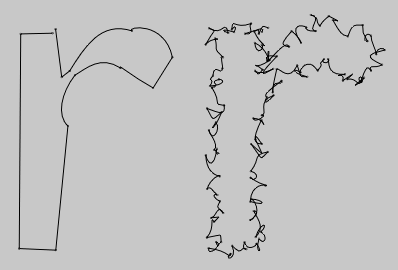
`.newLineByStroking(thickness#1, join0, cap#0, miter1, dash#None, phase0)`

Produce the line created by carefully stroking this line

This uses Java's very carefully implemented stroking code to produce a new FLine that captures the geometry produced by thickening (and end-capping, miter-limiting and dashing etc.) a line. Otherwise, .thickness is a cosmetic (and sometimes not that pretty looking) affair. Once you have this geometry you can subject it to further transformation and analysis. You'll want to look at the docs for Java's BasicStroke to get a sense of what the parameters do.

Example

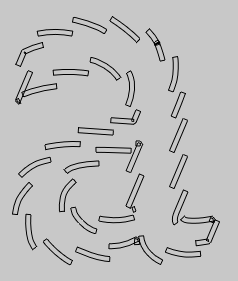
f = FLine().appendVectorText2("a", 0, 0, size=500)
f = f.newLineByStroking(thickness=5, miter=1, dash=(35,1))
segments = f.segment()
for n in segments:
    n += CFrame(r=0.4, center=n)
    _self.lines.add(n)

`.newLineBySubdivision()`

Converts all segments to curves then subdivides them in two

Example

_self.lines.clear()
for noise in [0, 5, 10, 20]:
    f = FLine().appendVectorText2("a", 0, 0, size=500)
    f(color=Color4(0,0,0,0.2))
    _self.lines.add(f)
    f.pointed=1
    
    for n in range(0, 4):
        f = f.newLineBySubdivision()
        f.filterPositions2(lambda x,y : Vector2(x,y).noise(noise))
        f += Vector2(200,0)
        _self.lines.add(f)