Simple Linear Algebra

Somewhere on the path between computer science and art inevitably lies the town of linear algebra: Vectors, rotations, matrices and so on. Field comes with a number of well-populated classes to make manipulating these things slightly less tedious.

Here's a quick and incomplete set of examples to give you a flavor of Vector2, which is used to represent a point or a direction in 2d space:

v1 = Vector2() # a vector at 0,0
v2 = Vector2(1, -2.5) # a vector at 1, -2.5

#they act a lot like Python tuples
print v2[0], v2.x # prints 1, 1
print v2[1], v2.y # prints -2.5, -2.5

#which mean you can pass them to PLine methods using * notation
PLine().moveTo( *v2 ) # is the same as .moveTo(1, -2.5)

v3 = v1+v2 # vectors can be added
v4 = v2*2.0 # vectors can be scaled
v5 = v2*v1 # vectors can be element-wise multipled
v1 += Vector2(5,5) #vectors can be mutated in place

Vector2 also has all manner of useful methods:

v1.normalize() # makes the length 1
v1.rotateBy(1) # angle in radians
dot = v1.dot(v2) # dot product
angle = v1.angle(v2) # the angle between v1 and v2
v6 = v1.orthogonal() # a vector2 that's at right angles to this one
v1.projectOut(v2) # remove part of the vector that's pointing in the direction v2

v1.interpolate(v2, 0.25) # move 25% of the way towards v2

By convention, any method that doesn't have anything better to return, returns the Vector2 that it operated on. This means that you can chain things together:

print v1.normalize().scale(5).projectOut(v2)+v3

Likewise, Vector3, Vector4, Color4, VectorN (an 'any dimension' Vector). See also Quaternion.

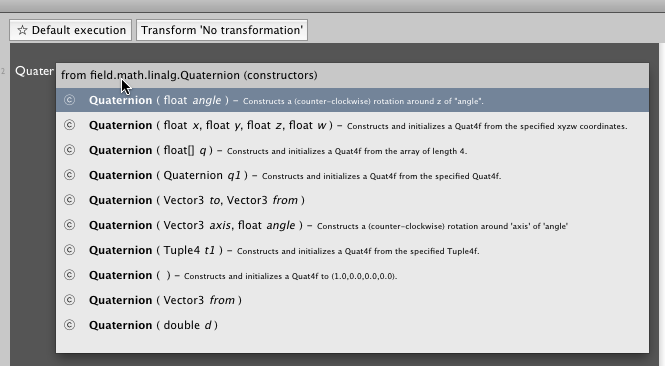
"See also?" Yes, Field contains its best source of documentation about this kind of thing: autocompletion is always the most authoritative way of getting info on these kinds of classes. Since it reads the source files that are ultimately compiled into your Vector2, it's never out of date and always complete. Also, don't miss right-click "open in Eclipse" and "search openendedgroup.com/field" options in the text editor.

For example, wondering how to get a Quaternion? press command-period after typing Quater:

Finally, Vector2,3,4,N can be "sliced" as in Python lists:

v = Vector4(1,2,3,4)
print v[:] # prints [1,2,3,4]

v[:] = (4,3,2,1) # sets this vector to a new value
print v # prints [4,3,2,1]

print v[0:2] # prints [4,3]

This is sometimes very useful for setting the values inside a VectorX very tersely.

This means that they can also be passed into functions for argument lists:

FLine().moveTo(*(a+b)*0.2)

Is equivalent to (and faster than):

FLine().moveTo( ((a+b)*0.2).x, ((a+b)*0.2).y, ((a+b)*0.2).z)

CFrame

CFrame is Field's coordinate frame factory function. Coordinate frames are useful for describing combinations of transformations in 3d spaces — compositions of rotations, translations and scales. Two things that you need to know about CFrames — firstly, is that the function you get them from tries to be maximally helpful; secondly, you can multiply them together to create new ones. First the function:

CFrame(r=Quaternion(), s=Vector3(1,1,1), t=Vector3(0,0,0), center=None)

CFrame is very obliging when it comes to the types of the things that you pass in. Here's a rotation of Pi/2 around the z axis:

r = CFrame(r=Math.PI/2)

A uniform scale of 0.5 around the point Vector3(100, 20, 40)

r = CFrame(s=0.5, center=Vector3(100,20,40))

CFrame will take anything for 'r' that we have a constructor for in Quaternion. Here's a rotation that takes the y-axis over to the x-axis:

r = CFrame(r=[Vector3(1,0,0),Vector3(0,1,0)])
print r * Vector3(0,1,0) # -- prints something close to [1,0,0]

Secondly, these things can be multiplied together:

r1 = CFrame(r=[Vector3(1,0,0),Vector3(0,1,0)])
r2 = CFrame(s=0.5, center=Vector3(100,0,0))
r3 = CFrame(t=Vector3(0,50,0))

total = r3*r2*r1

print total * Vector3(0,1,0) # -- prints [50,50,0]

Mentally you should think of multiplication as producing a machine. The Vector3 goes in the right hand side and comes out the left had side, passing through each of the operations in turn.