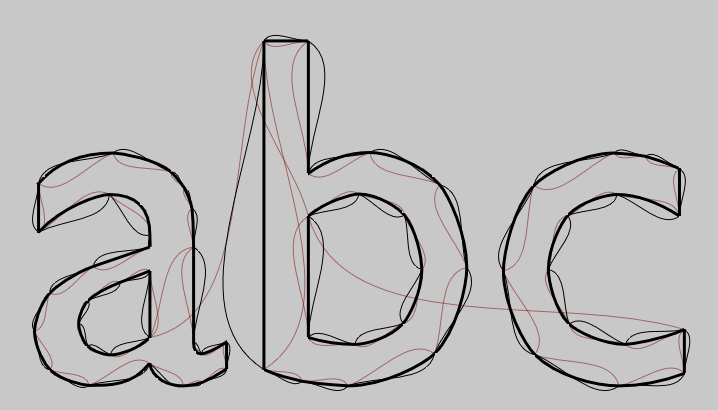FLine Node reference

FLine geometry containers are made up of control nodes. Roughly speaking, you get one control node for every .moveTo(...), .lineTo(...), or .cubicTo(...) you issue. Nodes have positions: 1 in the case of .moveTo or .lineTo or 3 in the case of .cubicTo. This code illustrates:

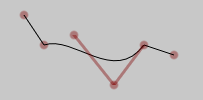
f = FLine().moveTo(10,10).lineTo(30,40).cubicTo(60,30,100,80, 130, 40).lineTo(160,50)
_self.lines.add(f)
for n in f.nodes:
    dots = FLine(pointed=1, pointSize=10, thickness=3, color=Color4(0.5, 0, 0, 0.4))
    for q in n.points():
        dots.lineTo(*q)
    _self.lines.add(dots)

This results in four nodes .moveTo(), .lineTo(), .cubicTo(), .lineTo()

As you can see from the code above you can access, inspect and modify the nodes of an FLine by accessing elements of the .nodes array. The page collects useful methods that you can perform on a node (an instance of CachedLine.Event), but as always, you can get the most complete, most up-to-date list through autocompletion.

.arbitraryProperty_v="peach"

You can set and get arbitrary properties on nodes. By convention they have the _v suffix (since this is what FLine uses to indicate that you want to set a property on the most recently created node). Some properties are handled as special signals to Field to do interesting things (change point styles, draw text etc...) take a look at the list.

node +# CFrame(r0.2)

You can transform nodes using CFrame instances, as well as Quaternions and Vector3 and Vector2 (see SimpleLinearAlgebra for an overview of this zoo). Transforming nodes and setting properties on them accounts for basically everything you want to do at this level with lines. Some examples:

f = FLine()
for n in floatRange(0, 10, 10):
    f.cubicTo(n*14, n*20, n*20, n*14, n*20, n*20)
_self.lines.add(f)

f = f.copy()
f.color=Color4(0.5, 0, 0, 1.0)
for n in range(len(f.nodes)):
    f.nodes[n] += Vector2(n*10,0)
_self.lines.add(f)

f = f.copy()
f.color=Color4(0, 0, 0.5, 1.0)
for n in range(len(f.nodes)):
    f.nodes[n] += Quaternion(-n*0.04)
    f.nodes[n] += Vector2(-n*4,0)
_self.lines.add(f)

CFrame also accepts FLine nodes for transform centers, which yields this pattern here (to have rotations and scales centered on the "head" of the line, see below):

for t in range(0, 20):
    f = f.copy()
    for n in f.nodes:
        n += CFrame(r=-Math.PI/20, center=n.head())
    _self.lines.add(f)

.position()

.setPosition(x,y[,z])

Gets or sets the position (end-point) of this node. This is a Vector3 (see SimpleLinearAlgebra for more). If you really want a Vector2 use .position2().

.isCubic()

Returns 1 if this is a cubic spline segment. Otherwise, returns 0.

.isConnected()

Returns 1 if this is a cubic spline segment or a line. Otherwise, returns 0.

.control1(), .setControl1(x,y[,z]), .control2(), .setControl2(x,y[,z])

Gets or sets the first or second control points of a node if it has them.

.points(), .setPoints([c1,c2,],p)

Gets or sets all the points (all the Vector3 positions) in this node. Either 1 (for .moveTo or .lineTo) or 3 (.cubicTo).

.next(), .previous(), .head()

These three functions navigate between nodes, next() and previous() are self explanatory — the nodes are a list, these return the previous and the next node in the list. head() goes backwards but only if this node is actually connected to the previous node, otherwise it returns the current node. Thus .head() of a .moveTo() is that .moveTo() not some potentially unrelated previous node.

This code and image illustrate the difference:

_self.lines.clear()
f = FLine().appendVectorText2("abc", 0, 0, size=500)
f.thickness=3
_self.lines.add(f)

for n in f.nodes:
    p = n.head() # -- head can never be null
    f = FLine().moveTo(*n.position()).polarCubicTo(0,1,-1,1,p.position().x, p.position().y)
    _self.lines.add(f)

    p = n.previous()
    if p: # -- previous can be null
        f = FLine().moveTo(*n.position()).polarCubicTo(0,1,1,1,p.position().x, p.position().y)
        f.color=Color4(0.5, 0, 0, 0.5)
        _self.lines.add(f)