
Generative Audio in Field
Recent versions of Field are builded with a new realtime audio framework that lets you write low-level code to create and manipulate sound directly. Think of this as the audio analogs of Stage and FLine. Before we get started exploring the basic functions of this framework, we’ll need a few core ideas.
1. Audio is made and processed in chunks
The fundamental unit of audio — audio’s pixel — if you will is the sample. For our purposes here we’ll think of this as a number between -1 and 1. You can get far enough by thinking of this as the position of the speaker cone in a loud-speaker as it wobbles back and forth or of the diaphragm of a microphone or the height / depth of a groove on a phonograph. This number represents a tiny approximate, instantaneous snapshot of this ‘position’, one lasting, in our case, 1/48000th of a second. By building up seconds and minutes of sound out of these millions of samples we achieve sufficient resolution to fool our ear (and speaker cone), in much the same way as we can force the perception of motion out of the sequential presentation of images.
Because of a host of technical reasons real-time sound software and hardware groups these samples together into ‘frames’ (or ‘chunks’ or ‘vectors’) and processes a whole group of them together. A chunk of 2000 or so sequential samples represents 1/24th of a second.
Field follows this dominant ‘chunk’ paradigm for all of the same reasons as almost everything else does: efficiency. Efficiency drives many of the concerns that torque the way code for audio is written. In particular, audio processing is much more time sensitive than most imagery: deliver a frame from the graphics hardware late and people might notice a tiny glitch, deliver an audio chunk late and there’s a rip of static. This means that we can’t quite write low-level audio code anywhere in Field, we have to put it into special boxes, that run in a special way.
2. Start with a Mixer box
Note: delete any previous Sound playing boxes before you add a Mixer, and restart Field
So, let’s build and playback a chunk of sound. First we need a ‘mixer’ box. This will represent our software connection to the sound output hardware. You can get one by the same was as you get a stage — by ctrl-space ‘insert from workspace’ and selecting audio.mixer.

To make a box that can execute inside the ‘audio loop’ connect a new box to mixer by holding down ‘g’ and dragging:
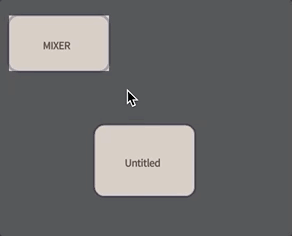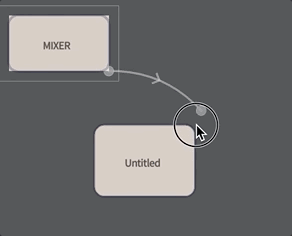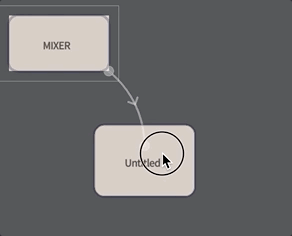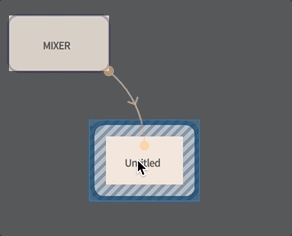
Make sure you drag from the mixer to the box and not the other way around (the metaphor: the Mixer ‘governs’ the box, the Mixer’s contents flow’s ‘downwards’ through the arrow).
3. Don’t use _.stage.frame(), use _r
Now we have a box that runs just like any other box you’ve made in Field except it does so in the ‘audio loop’, with one exception: we can’t use _.stage.frame() and the like to interleave animation frames into our code — since we don’t know when those animations frames might be happening. Our code is executing whenever the audio hardware on the computer needs more audio.
In a box that’s connected to the mixer:
var buffer = $.newBuffer()
for(var i=0;i<buffer.length;i++)
{
buffer[i] = Math.random()
}
$.output = buffer If we execute that (option-zero or option-up) we’ll get a tiny 1/24th of a second loud burst of ‘white noise’ — this is what random numbers sound like.
It’s worth going through this very straightforward code line by line.
First we need to make an audio chunk to put our samples into:
var buffer = $.newBuffer()We get this audio chunk from a new special object called $ (short for $ample perhaps?).
Then for every sample slot that’s in it:
for(var i=0;i<buffer.length;i++)… we’ll slot in a random number
for(var i=0;i<buffer.length;i++)
{
buffer[i] = Math.random()
}Finally, we’ll tell field that we want that to be the ‘output’ of this box — otherwise we’ll hear nothing
$.output = buffer Next we want to obviously make a more sustained sound than this! For that we’ll need to install something into the audio loop that can run by itself. We do this by declaring a function in our box called _r
_r = () => {
var output = $.newBuffer()
for(var i=0;i<output.length;i++)
{
output[i] = Math.random()-0.5
}
$.output = output * 0.1
}Since we’re ‘launching’ this box — letting it run on and on forever until we stop it — we need to use option-up rather than just option_zero (which would happily define _r to be our function and then do nothing more with it). If we do so, we’ll end up with a steady stream of white noise (press option_down to stop the box!).
Not being able to use _.stage.frame() means that we need to be smarter about our logic and control. Whatever _r is left defined after your code has run is the _r that Field uses to compute audio frames. See the cookbook below for some examples.
Carefull observers will note that we’re multiplying buffer by 0.1 which is, strictly speaking, not allowed in JavaScript. It’s for moments like this that we build our own programming environment. We can add, multiply, subtract even divide buffers with numbers and other buffers.
Finally, before we move on too far, let’s add one more line:
_r = () => {
var output = $.newBuffer()
for(var i=0;i<output.length;i++)
{
output[i] = Math.random()-0.5
}
$.output = output * 0.1
_.scope(output)
}This lets us see the raw waveform stuck next to the box we’re writing code in:

4. Making a Sine wave
Let’s slowly get more musical.
var p = 0
_r = () => {
var output = $.newBuffer()
for(var i=0;i<output.length;i++)
{
output[i] = Math.sin(p)
p = p+0.1
}
$.output = output * 0.1
_.scope(output)
}This gives us a sin wave that we hear as a (very) pure tone. If you change that p = p+0.1 to p = p+0.01 this tone will go down (a lot) in frequency (possibly below your range of hearing on laptop speakers). Similarly p = p+0.2 doubles the ‘pitch’ of our tone.
5. Change is difficult
Discontinuity in animation is to be expected — two frames of an animation are different, and that’s what yields motion. But discontinuity in audio sound bad. Worse, it’s easy to be discontinuous by accident. You might be tempted to write:
// this code is WRONG, don't do this
_r = () => {
var p = 0
var output = $.newBuffer()
for(var i=0;i<output.length;i++)
{
output[i] = Math.sin(p)
p = p+0.1
}
$.output = output * 0.1
_.scope(output)
}Or, similarly:
// this code is WRONG, don't do this
_r = () => {
var output = $.newBuffer()
for(var i=0;i<output.length;i++)
{
output[i] = Math.sin(i/10)
}
$.output = output * 0.1
_.scope(output)
}And you’ll hear a fast clicking noise superposed ontop of your pretty sin tone. What’s gone wrong is that, unless you guess very carefully with the /10 in your Math.sin the last sample of a chunk is very different from the first sample of the next chunk. This discontinuity causes a click as the speaker cone suddenly rushes to a new position as fast as it can. We need our samples to be smooth across chunk boundaries.
Secondly, the same situation can occur when changing things outside our _r loop. Let’s go back to our working sine wave:
var p = 0
var amplitude = 0.1
_r = () => {
var output = $.newBuffer()
for(var i=0;i<output.length;i++)
{
output[i] = Math.sin(p)
p = p+0.1
}
$.output = output * amplitude
_.scope(output)
}Now we can change the value of amplitude in true “Field style”, by editing 0.1 and changing it to 0.43 and pressing option-return while our box is running (option-up). But every time we do so we here that same ‘click’ again! What’s happening? The same thing. In between audio chunks we are changing amplitude, which means that likely the first sample of the chunk that’s made with the new value of amplitude is going to be different from the last sample of the previous chunk (made with the old value of amplitude). What to do?Well, what we really need to do is smoothly slide the value of amplitude that our code sees over a short period of time.
Well, we could do it by hand:
var p = 0
var amplitude = 0.1
var smoothAmplitude = amplitude
_r = () => {
var output = $.newBuffer()
for(var i=0;i<output.length;i++)
{
smoothAmplitude = 0.99*smoothAmplitude + 0.01*amplitude
output[i] = Math.sin(p)*smoothAmplitude
p = p+0.1
}
$.output = output
_.scope(output)
}But: Yuck! We’ve had to add another variable outside our function and stuck some complicated looking stuff inside our sample-level loop. Since this happens almost all the time when communicating with the insides of an audio loop, Field has special help for doing this:
var amplitude = 0.1
var p = 0
_r = () => {
var output = $.newBuffer()
for(var i=0;i<output.length;i++)
{
output[i] = Math.sin(p)
p = p+0.1
}
$.output = output * Line(amplitude)
_.scope(output)
}Line is a audio ‘unit’ that magically interpolates its input across time. You’ll see all of the current units listed below in the reference section. Line is called line because it moves to the current value of ‘amplitude’ in a straight line (across a single audio chunk).
6. Music (theory) is math
Now that we know how to change things, you might be wondering what pitch p = p + 0.1 corresponds to. First let’s realize that Field runs its sample rate at 48000 samples per second. Let’s do the math!
Each sample lasts 1/48000th of a second, p advances 0.1 each sample so in one second p has advanced by 4800. Sin has a period of 2*Math.PI, and 4800 is 4800/(2*Math.PI) periods which is 763.94-ish. Its doing those 763.94ish periods in one second, so our ‘oscillator’ is oscilating at 763.94 Hertz (the fancy name for frequency aka cycles-per-second). 763.94 Hz is a pitch that we can hear (our hearing range is roughly 20 Hz to 20,000 Hz, unless they invented the portable music player during your childhood, in which case it’s more like 18,000Hz).
Back to our code, let’s rewrite it so that we are actually using pitches measured in Hz:
var amplitude = 0.1
var p = 0
_r = () => {
var output = $.newBuffer()
var f = 440 * Math.PI * 2 / 48000
for(var i=0;i<output.length;i++)
{
output[i] = Math.sin(p)
p = p+f
}
$.output = output * Line(amplitude)
_.scope(output)
}I’ve switched to a pitch of 440 Hz. Why? That’s a note called a concert A.
If we try twice that, 880 Hz, we get the ‘A’ one ‘octave’ above. Suddenly we’re doing music theory. That ‘doubling’ is what an octave is, from any pitch we like we can go ‘up’ and octave by doubling it (and down an octave by halfing it).
I’m aware that this section is problematic for those of you that haven’t learned an instrument / how to read music. None of the western note name systems and notations are truely defensible (12 notes in an ‘oct’ave? not 8? Why A, A#, B, C, C#, D … where’s the B# and so on). What we are looking at is a notational pracice that’s grown organically and solidified over a period of 500 years or so.
There are 12 notes in an octave in the western classical tradition, these 12 notes fit into that factor of two. Thinking about this both carefully and with a willingness to approximate (and to ignore important controversies over more precise tunings that have raged for millenia) we end up with this math:
var amplitude = 0.1
var p = 0
var note = 0
_r = () => {
var output = $.newBuffer()
var f = 440 * Math.pow(2, note/12.0) * Math.PI * 2 / 48000
for(var i=0;i<output.length;i++)
{
output[i] = Math.sin(p)
p = p+f
}
$.output = output * Line(amplitude)
_.scope(output)
}With note=0 we have a middle A, note=1 gives us an A#, note=2 a B, note=3 a C and so on.
A faster way to a pure tone
While Field will let you make sound from first principles sometimes that’s a little too low level. Perhaps you just need a sine wave. Let’s try this instead:
var amplitude = 1.0
_r = () => {
var output = Sin(440, amplitude)
$.output = output
_.scope(output)
}Tada! Sin contains all of the magic and logic to maintain a continuous Sin at the frequency 440 with (interpolated) amplitude.
Now we can experiement:
var amplitude = 1.0
_r = () => {
var output = (Sin(440, amplitude) + Sin(880, amplitude/2.0)) * 0.2
$.output = output
_.scope(output)
}Gives us something that’s beginning to sound a little like an organ.
There are a few of these audio units like Sin built into Field (and you can make audio units out of boxes to build your own). Let’s look at them:
Line(x)
Smoothly interpolate over an audio chunk the value of ‘x’. Line is useful in many situations where change might occur, this includes many places that you might not expect it to crop up. Consider this code:
var t = 10
_r = () => {
var output = $.newBuffer()
if (t>5)
{
$.output = Sin(440)
}
else
{
$.output = Sin(880)
}
t = t*0.9
}The intention here is to have a tone that starts as Sin(440) and changes to Sin(880) instantanously when t reaches the right value. Alas, things are not so simple. At the exact moment when t switches over, we might hear a discontinuity glitch. What we need is something like this:
var t = 10
_r = () => {
var output = $.newBuffer()
$.output = Sin(440) * Line(t>5) + Sin(880) * Line(t<=5)
t = t*0.9
}This mixes the two signals Sin(440) and Sin(880) together. Almost all of the time only one of these signals will be ‘sounding’ except for a moment of crossfade when t switches over.
Line0(x)
Line0 is just like Line except that it always starts initially from 0.
Sin(frequency, amplitude = 1.0, phaseOffset = 0.0)
Sin yields a sine wave with particular freqency and amplitude. Sending numbers to phaseOffset lets you add a kind of vibrato to the oscillator. You don’t need to specify amplitude or phaseOffset if you don’t want to (that’s what the = 1.0 and = 0.0 tell you here, they are the values if you don’t write them in). phaseOffset let’s you perturb the phase of our oscillator. Since our ears are (largely) insenstive to phase, we can only here this when it changes.
Play(filename, speed = 1.0, offset = 0.0, looping = true)
Play plays a .wav file from disk with speed and sample offset. Control the speed to change the speed and pitch of the playback (a value of 0.5 plays everything an octave lower and twice as slow). Changing the offset (in samples) lets you ‘scratch’ a sound or start some of the way into it.
You can dig out a standard Field sound analysis object from your Play:
var output = Play("/Users/marc/Desktop/Pockets_w_excerpt.wav")
var player = output.source()
var energy = player.analysis().getNormalized("spectral_energy", player.time())
$.output = output Note we have to get time from our player (not from the red line), since only it knows what part of the wave file is being played when.
Sometimes when using Play Field’s default behavior — to run boxes from the state that they were last at — isn’t what you want. You want a subsequent option_up to start again from the beginning. Putting $.clear() outside of your _r loop will achieve this.
Play also gives you some addition insight into what it’s playing back. This code here shows you how to get the current playing time and duration from a playing object.
_r = () => {
var p = Play("bananaa.wa"v)
// where did the audiochunk p come from ?
var player = p.source()
var time = player.time()
var loopedTime = player.loopingTime()
var duration = player.duration()
}Delay(signal, delayInSamples)
Delays a signal by a certain number of samples. This is a fundemental building block of many more sophisticated synthesis algorithms, and can be a quick way to create complex sounds.
For example:
var t = 1
_r = () => {
var o = Sin(440) * Line0(t)
o = o + Delay(o, 10000*Math.random())
t = t*0.9
$.output = o * 0.2
}FilterHigh(signal, frequency, resonance)
FilterLow(signal, frequency, resonance)
FilterBand(signal, frequency, resonance)
FilterNotch(signal, frequency, resonance)
FilterPeak(signal, frequency, resonance)
FilterAll(signal, frequency, resonance)
These all provide resonant filters that knock out or keep part of the spectrum of the signal. The resonance parameter should be less than 1 unless you want the filter to be ear-shakingly unstable.
AutoGain(signal)
AutoGain will try to normalize the signal so that it’s roughly in range. For rapidly changing sounds this might still overshoot the capabilities of your speakers / ears. Consider something like $.output = AutoGain(signal)*0.1
Delay(signal, samples)
This delays a signal by samples number of samples (so, delay it by 48000 to delay the sound by a full second). samples can be non-integer in which case the signal will be interpolated correctly.
Grainulator
See the cookbook below. Grainulator works slightly different than these audio units (only because you can interact with the running object differently).
Microphone
Returns a audio chuck that just happens to have a set of values in it that come from your microphone(!). If you feed that directly back into $.output you’ll likely get some feedback / echo delay.
A cookbook
The aim here is to provide a view of sound production that’s satisfyingly low-level, yet easy enough to play around with that you can actually be productive. Two pieces of example code that tour various two popular synthesis algorithms.
FM Synthesis
The basis for every synth lead part of every pop-song legally recorded from 1983 to 1990, and the loss of more of my youth than I care to admit, ties two or more oscilators together with the first modulating the frequency (or phase) of the second.
var t = 400
_r = () => {
var f = 240+Sin(440)*t
ll = Sin(f)
$.output = AutoGain(ll)
}This can get out of hand quickly. In fact FM Synthesis’s core strength is in the circuitious but sensible routes it takes between sounds, rather than the sounds themselves:
var t = 40
_r = () => {
var f = 440+Sin(70)*t+Sin(1-t)*t*t
t = t*0.99
var ll = Sin(f*0.1)+Sin(f*2)*(40-t)
$.output = AutoGain(ll)
}Or:
var t = 40
_r = () => {
var f = 240+Sin(50-t)*t-t
var ll = 440+Sin(f)*10*t+Sin(f*t)*100
t = t*0.9
ll = Sin(ll)
$.output = AutoGain(ll)
}Karplus-Strong percussion
This percussion algorithm starts with a set of numbers (usually with white noise in them) and successively filters them while unspooling them out into audio chunks.
// random numbers
var numbers = []
// we'll have 150 of them
// this ends up controlling the pitch
var c = 150
for(var i=0;i<c;i++)
{
numbers.push(Math.random()-0.5)
}
var previous = 0
// this ends up controlling the speed of the decay
var alpha = 0.9
var index = 0
_r = () => {
let output = $.newBuffer()
var c = output.length
for(var i=0;i<c;i++)
{
var z = (index++)%numbers.length
var sample = numbers[z]
previous = alpha*previous + (1-alpha)*sample
output[i] = previous
numbers[z] = previous
}
output = FilterPeak(output, 440, 0.9)*1
$.output = output*1
}Granular synthesis
A ‘grain’ is a tiny snippet of audio, often taken out of a much longer sample. By adding together a swarm of grains that take different pieces of an underlying sample we can generate new audio that retains some of the ‘sound’ of a sample but possess a different temporal structure.
A grain needs a ‘time’ (from the underlying sample), a duration, a ‘speed/pitch’ (does the grain play the sample out at the ‘correct’ speed or slower / faster, negative numbers go backwards), and a parameter that controls how abrupt the ‘window’ around the sample is (does it suddeny cut in and out or does it fade slowly in and out?).
Finally, it’s helpful to cap the total number of grains that can be ‘in play’ at any one time (so that your code doesn’t have to keep track). 40 is easily achivable on my laptop.
// import the Grainulator, it was too new to make the release
var Grainulator = Java.type("auw.standard.Grainulator")
// build a new Grainulator on a sound sample
var g = new Grainulator().apply("/Users/marc/Desktop/TC01_mono.wav")
var t = 0
_r = () => {
if (Math.random()<0.5)
{
// parameters to addGrain are
// time, duration, volume, speed, windowSharpness, maximum number of grains
g.addGrain(5+Math.sin(t)*1, 0.3, 0.1, 0.5, 2, 40)
}
t += 0.01
var o = g.compute() * 1.0
// sweep filter
//o = FilterHigh(o, 1440*(1.1+Math.sin(t*1)), 0.99) * 1.0
_.scope(o*20)
$.output = o *6.3
}The code above is randomly taking a grain of audio from around 5 seconds in to the sound file; each grain lasts 0.3 seconds, it has a volume of 10%, it’s played at half speed (and, thus, half pitch).
Beats!
What about something with a bit of rhythm? Well, we can divide up time into a grid (the basis of rhythm) quite easily if we are willing to limit our selection of tempos to the audio chuck rate (so, in units of 1/24). For example, take this code here:
var numbers = []
var index = 0
// function to re-'pluck' our
// string
var init = (q, n) => {
numbers = []
var c = n
for(var i=0;i<c;i++)
{
numbers.push((Math.random()-0.5)*q)
}
index = 0
}
init(1, 150)
var previous = 0
// decay speed
var alpha = 0.9
var f = 0
_r = () => {
// standard K-S percussion synth
let output = $.newBuffer()
var c = output.length
for(var i=0;i<c;i++)
{
var z = (index++)%numbers.length
var sample = numbers[z]
previous = alpha*previous + (1-alpha)*sample
output[i] = previous
numbers[z] = previous
}
// much massaging here of the sound
output = FilterPeak(output, 440*(1.3+Math.sin(f/11)), 0.99)*0.3
output = output + output * Sin(40) + Sin(output*44*(f%5))*output
output = FilterHigh(output, 1000, 0.1) * 1.0
$.output = AutoGain(output)*0.2
_.scope(output*0.3)
// this is our rhythm generator
if (f%4==0)
{
init( 4-(f/4) % 8, 305+f%19)
if (f%12==0)
{
init(10, 1200*(1 + (f%30)/12))
}
}
f = f + 1
}Throughout this code, but mainly at the end, we build a ‘rhythm’ out of a variable f that increments with every audio chunk. When f%4==0 we pluck our ‘karplus-strong’ string simulation again. When is f%4==0 ? Every fourth chunk. % is the modulo operator (think of it as a ‘remainder operator’ 17 % 4 == 1 because 17 / 4 is 4 remainder 1). When both f%4==0 and f%12==0 we pluck very differently. f%19 and f%30 and f%5 are chosen to cycle out of sync with f%4 which causes this small amount of code to spit out a sound that is constantly shifting.
Here’s another example, this time driving a subtractive synthesis algorithm:
Subtractive Synthesis
var Distort = Java.type("auw.standard.Distort")
var t = 1
$.clear()
var f = 0
_r = () => {
let output = $.newBuffer()
var c = output.length
for(var i=0;i<c;i++)
{
output[i] = Math.random()
}
var o = output
var b = 220/2
// you can comment out each of these stages to try
// to head which part of the sound they are removing
o = o + FilterLow(o, b, 0.9) *4.5 +Delay(FilterPeak(o, b*5, 0.9) *0.5*Line(t), Math.random()*100*Math.sin(f/4))
o = FilterPeak(o, b*2+t*100, 0.99) *0.5 +o*Sin(1114)*0.
o = FilterPeak(o, b*(3+Math.sin(f/14)), 0.99) *0.5
o = FilterPeak(o, b*10+t*1000, 0.99) *0.5
o = o+Line(t)*Delay(FilterPeak(o, b*9+b, 0.999) *0.5*Line(t), 400*(Math.sin(10*t)+1))
o = (FilterAll(o, 8000, 0.9) * 1.0 + o)
o = (FilterLow(o, 8000*t, 0.9) * 1.0)
_.scope(o *0.01)
t = t*0.99
$.output = AutoGain(o)*0.3
// rhythm step sequencer
f++
if (f%4==0) t= 2
if (f%12==0) t= 3.3
if (f%16==0) t= 4
}Stereo?
So far absolutely all of this page has been producing mono sound signals. But you have two ears (and, likely, two speakers on your laptop / headphones).
Field is actually producing sounds in a very simple ‘simulated’ acoustic environment. To set the ‘position’ of the mixer, and all of the sounds mixed into it:
// to the left
_.mixer.io.setSourcePosition(vec(2,0,0)) This position can be ‘animated’ using the usual tricks.
Finally, adding a tiny text file with the name .alsoftrc into your ‘home’ directory that contains the following single line:
hrtf = trueWill turn on the HRTF part of the simulation — this delays and filters the sound you hear in each ear by a simulation of the effects of your outer ear. This means, for headphones and the right sources, the presence of the audio is likely to ‘feel’ like it’s coming from the right place.